However, products came in different unit sizes. For instance, if a customer chose a paint brand that came in 1 quart, 1 gallon, and 5 gallon sizes, there were many combinations of those sizes that would meet their coverage needs. How to choose a combination? In this case, choosing the combination of container sizes that minimized the price was the way to go. This ensured that the client had a competitive price.
Larger containers are usually proportionately cheaper, so it's tempting to just calculate the quantities by favoring the largest units first and working down. However, this isn't always the case. Maybe the store has sales that can make smaller units cheaper. Or sometimes there aren't enough of the larger units to meet the customer's needs. Or maybe the store's pricing structure is such that the larger containers aren't proportionately cheaper after all. I've seen all these happen.
Constrained Optimization to the Rescue!
Now the problem gets more challenging. And even if it weren't hard, why write the code? We're programmers and good programmers reuse. Fortunately, there are tools out there to solve problems like this and a whole lot more. These are constrained optimization packages.
Constrained Optimization is figuring out what values are needed to minimize or maximize some function while adhering to one or more constraints. These values are the outputs of the process and are called Decision Variables. Let's phrase the example above in constrained optimization terms.
Assume the following...
p0..pn−1: the price for each size paint can.
s0..sn−1: the # of each size paint can in stock.
c0..cn−1: the area each size paint can covers.
a: the total project area.

Then we can phrase our problem as the task of finding the number of each size of paint can to buy that minimizes price, provided the paint cans cover the project area and we don't exceed the amount in stock. Or to put it a bit more mathematically...
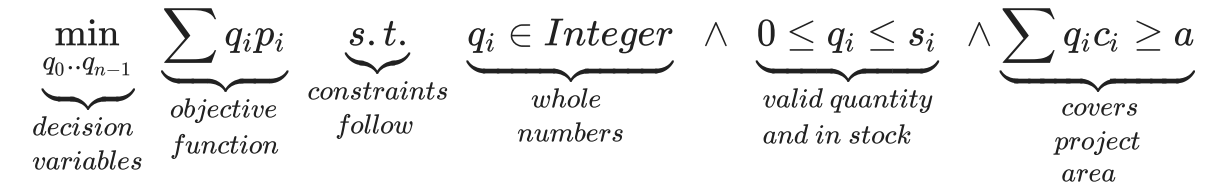
Key Terms Defined
Decision Variables
Our outputs are the results the optimization is to produce. These have a type and range. In this case, it's an integer, since it's a count of containers, and its value ranges from 0 (nothing to buy) up to what's available in stock.
q0..qn−1 are the quantity of each container to buy.
Minimize
The expression to minimize, ∑qipi. This expression is called the objective function, and in this case it's the total price. The optimization package will set the values of qty such that the total price is as low as it can be.
Constraints
This is the expression ∑qic i ≥ a. These are the conditions that any solution must meet. In this case, it states that the total coverage of the quantities chosen meets or exceeds the project area. We could add many more constraints, and much of the power of constrained optimization is in the wise (or even clever) application of constraints. In fact, the domain of our decision variables can be worded as constraints.
The Objective Function
Your objective function can be quite complex, but as you get into more complex objective functions involving higher powers, you need to keep a few things in mind:
You'll need a solver that can handle that type of problem. Solvers are what actually find our solutions. Some solvers are meant for linear problems, some for non-linear problems, some specialize in integers, and so on.
You might not be able to find an optimal solution. Instead, you may get feasible solutions or no solutions at all.
It may take longer to run the optimization, especially for non-linear problems.
Let's talk about each of these issues in turn.
The Solver
Packages that handle constrained optimization will either be configured for specific types of problems or will expect you to tell them which kind of solver to use. Often, the packages will have different solvers to choose from, but sometimes you may be expected to find and install your own solver.
Finding the Solution
Some optimization problems can take an extremely long time to solve, so long that getting an optimal solution is not feasible. For these kinds of problems, you may end up with a feasible solution, but not an optimal one. That's not as bad as it sounds, because since the problem is that complex, it's unlikely anyone else is getting an optimal solution. Of course, you may not get a solution at all.
Performance
The solution time for constrained optimization problems can vary from under a second to... well, let's just say long enough that no one's going to wait for it 😀. Packages today are quite efficient, and we of course have lots of computing horsepower at our disposal, but there are still some problems that will tax even the most powerful hardware. For a lot of "straight-forward" applications we don't need to worry about this. But keep this in the back of your mind when you decide to approach a constrained optimization problem.
Conclusion
The combination of objective function and constraints can open the door to a wide variety of problems we can now solve. And as stated previously, there are packages out there where we can feed them the problem to solve and they'll do it for us. I'll get into that in the next article. For now, I just want you to get an overview of this class of problems and the language around it. I want to do this for the following reasons:
To prepare you for the article(s) to come, where I delve into using a package to solve this problem.
To know the lingo so you have to search terms and a language to express your problems.
To apply constrained optimization thinking to problems you face; many problems are constrained optimization ones in disguise or can be converted to them.
Tune in next time when I get into some code!




