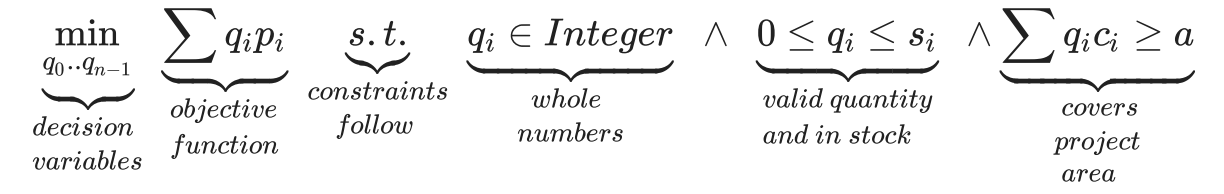Cependant, les produits sont disponibles en différentes tailles. Par exemple, si un client choisit une marque de peinture disponible en 1 quart, 1 gallon et 5 gallons, il existe de nombreuses combinaisons de ces tailles qui répondraient à ses besoins en matière de couverture. Comment choisir une combinaison ? Dans ce cas, la solution consistait à choisir la combinaison de contenants la moins chère possible. Cela a permis au client de bénéficier d'un prix compétitif.
Il est donc tentant de calculer les quantités en privilégiant d'abord les unités les plus grandes, puis les plus petites. Mais ce n'est pas toujours le cas. Il se peut que le magasin organise des soldes qui permettent de réduire le prix des petites unités. Il arrive aussi que les grandes unités ne soient pas assez nombreuses pour répondre aux besoins du client. Ou encore, la structure de prix du magasin est telle que les grands contenants ne sont finalement pas proportionnellement moins chers. J'ai vu tous ces cas de figure se produire.
L'optimisation sous contraintes à la rescousse !
Le problème devient alors plus complexe. Et même s'il n'était pas difficile, pourquoi écrire le code ? Nous sommes des programmeurs et les bons programmeurs réutilisent. Heureusement, il existe des outils permettant de résoudre des problèmes de ce type et bien d'autres encore. Il s'agit de progiciels d'optimisation sous contrainte.
L'optimisation sous contrainte consiste à déterminer les valeurs nécessaires pour minimiser ou maximiser une fonction tout en respectant une ou plusieurs contraintes. Ces valeurs sont les résultats du processus et sont appelées Variables de décision. Formulons l'exemple ci-dessus en termes d'optimisation sous contrainte.
Supposons ce qui suit...
p0..pn-1 : le prix de chaque format de pot de peinture.
s0..sn-1 : le nombre de pots de peinture de chaque taille en stock.
c0..cn-1 : la surface couverte par chaque pot de peinture.
a : la surface totale du projet.
Nous pouvons alors formuler notre problème comme étant la tâche consistant à trouver le nombre de pots de peinture de chaque taille à acheter pour minimiser le prix, à condition que les pots de peinture couvrent la zone du projet et que nous ne dépassions pas la quantité en stock. Ou, pour le dire de manière un peu plus mathématique...
Définition des termes clés
Variables de décision
Nos produits sont les résultats que l'optimisation doit produire. Ils ont un type et un intervalle. Dans le cas présent, il s'agit d'un nombre entier, puisqu'il s'agit d'un nombre de conteneurs, et sa valeur s'étend de 0 (rien à acheter) à ce qui est disponible en stock.
q0..qn-1 sont les quantités de chaque conteneur à acheter.
Minimiser
L'expression à minimiser, ∑qipi. Cette expression est appelée fonction objectif et, dans le cas présent, il s'agit du prix total. Le progiciel d'optimisation fixera les valeurs de qty de manière à ce que le prix total soit le plus bas possible.
Contraintes
Voici l'expression ∑qic i ≥ a. Il s'agit des conditions auxquelles toute solution doit satisfaire. Dans le cas présent, elle indique que la couverture totale des quantités choisies est égale ou supérieure à la zone du projet. Nous pourrions ajouter de nombreuses autres contraintes, et une grande partie de la puissance de l'optimisation sous contraintes réside dans l'application judicieuse (ou même intelligente) des contraintes. En fait, le domaine de nos variables de décision peut être formulé comme des contraintes.
La fonction objective
Votre fonction objectif peut être assez complexe, mais à mesure que vous vous engagez dans des fonctions objectifs plus complexes impliquant des puissances plus élevées, vous devez garder certaines choses à l'esprit :
Vous aurez besoin d'un solveur capable de traiter ce type de problème. Les solveurs permettent de trouver les solutions. Certains solveurs sont conçus pour les problèmes linéaires, d'autres pour les problèmes non linéaires, d'autres encore sont spécialisés dans les nombres entiers, etc.
Il se peut que vous ne puissiez pas trouver une solution optimale. Il se peut que vous obteniez plutôt des solutions réalisables ou pas de solution du tout.
L'exécution de l'optimisation peut prendre plus de temps, en particulier pour les problèmes non linéaires.
Examinons chacun de ces problèmes tour à tour.
Le solveur
Les packages qui gèrent l'optimisation avec contraintes sont soit configurés pour des types de problèmes spécifiques, soit attendent que vous leur indiquiez le type de solveur à utiliser. Souvent, les paquets proposent différents solveurs, mais il peut arriver que l'on vous demande de trouver et d'installer votre propre solveur.
Trouver la solution
Certains problèmes d'optimisation peuvent être extrêmement longs à résoudre, à tel point qu'il n'est pas possible d'obtenir une solution optimale. Pour ce type de problèmes, vous pouvez obtenir une solution réalisable, mais pas une solution optimale. Ce n'est pas aussi grave que cela en a l'air, car le problème étant très complexe, il est peu probable que quelqu'un d'autre obtienne une solution optimale. Bien entendu, il se peut que vous n'obteniez aucune solution.
Performance
Le temps de résolution des problèmes d'optimisation sous contraintes peut varier de moins d'une seconde à... disons qu'il est suffisamment long pour que personne ne l'attende 😀. Les progiciels d'aujourd'hui sont assez efficaces, et nous disposons bien sûr d'une grande puissance de calcul, mais il y a encore des problèmes qui mettent à l'épreuve même le matériel le plus puissant. Pour un grand nombre d'applications "simples", nous n'avons pas besoin de nous préoccuper de ces problèmes. Mais gardez cela à l'esprit lorsque vous décidez d'aborder un problème d'optimisation avec contraintes.
Conclusion
La combinaison de la fonction objectif et des contraintes peut ouvrir la porte à une grande variété de problèmes que nous pouvons maintenant résoudre. Et comme indiqué précédemment, il existe des progiciels qui nous permettent de leur fournir le problème à résoudre et qui le font pour nous. J'y reviendrai dans le prochain article. Pour l'instant, je veux juste que vous ayez une vue d'ensemble de cette classe de problèmes et du langage qui l'entoure. Je le fais pour les raisons suivantes :
Pour vous préparer au(x) article(s) à venir, où j'approfondirai l'utilisation d'un package pour résoudre ce problème.
Connaître le jargon afin que vous puissiez rechercher des termes et un langage pour exprimer vos problèmes.
Appliquer la pensée de l'optimisation sous contrainte aux problèmes que vous rencontrez ; de nombreux problèmes sont des problèmes d'optimisation sous contrainte déguisés ou peuvent être convertis en problèmes d'optimisation sous contrainte.
Revenez la prochaine fois lorsque je me lancerai dans le code !