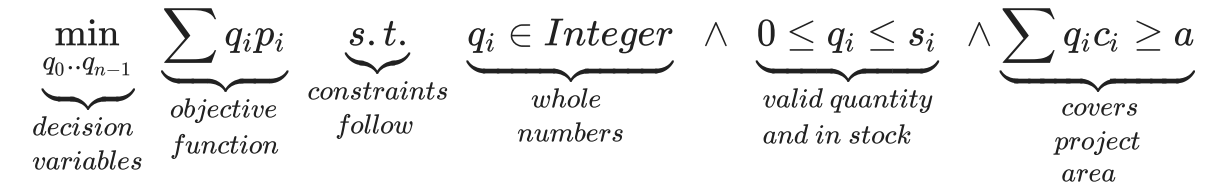Sin embargo, los productos se presentan en diferentes tamaños. Por ejemplo, si un cliente elige una marca de pintura que viene en tamaños de 1 litro, 1 galón y 5 galones, hay muchas combinaciones de esos tamaños que podrían satisfacer sus necesidades de cobertura. ¿Cómo elegir una combinación? En este caso, lo mejor era elegir la combinación de tamaños de envase que minimizara el precio. De este modo, el cliente se aseguraba un precio competitivo.
Los contenedores de mayor tamaño suelen ser proporcionalmente más baratos, por lo que resulta tentador calcular las cantidades dando prioridad a las unidades más grandes y reduciéndolas. Sin embargo, no siempre es así. Puede que en la tienda haya rebajas que abaraten las unidades más pequeñas. O a veces no hay suficientes unidades grandes para satisfacer las necesidades del cliente. O puede que la estructura de precios de la tienda sea tal que los envases más grandes no sean proporcionalmente más baratos después de todo. He visto cómo ocurrían todas estas cosas.
Optimización restringida al rescate
Ahora el problema se complica. Y aunque no fuera difícil, ¿para qué escribir el código? Somos programadores y los buenos programadores reutilizan. Afortunadamente, existen herramientas para resolver problemas como éste y muchos más. Son los paquetes de optimización restringida.
Optimización restringida consiste en averiguar qué valores son necesarios para minimizar o maximizar una función respetando una o varias restricciones. Estos valores son los resultados del proceso y se denominan variables de decisión. Formulemos el ejemplo anterior en términos de optimización con restricciones.
Supongamos lo siguiente
p0..pn-1: el precio de cada tamaño de lata de pintura.
s0..sn-1: el número de latas de pintura de cada tamaño en stock.
c0..cn-1: la superficie que cubre cada tamaño de bote de pintura.
a: la superficie total del proyecto.
Entonces podemos plantear nuestro problema como la tarea de encontrar el número de latas de pintura de cada tamaño a comprar que minimice el precio, siempre que las latas de pintura cubran el área del proyecto y no excedamos la cantidad en stock. O dicho de forma un poco más matemática...
Definición de términos clave
Variables de decisión
Nuestras salidas son los resultados que debe producir la optimización. Tienen un tipo y un rango. En este caso, es un número entero, ya que es un recuento de contenedores, y su valor oscila entre 0 (nada que comprar) hasta lo que está disponible en stock.
q0..qn-1 son la cantidad de cada contenedor a comprar.
Minimizar
La expresión a minimizar, ∑qipi. Esta expresión se llama función objetivo, y en este caso es el precio total. El paquete de optimización fijará los valores de qty de forma que el precio total sea lo más bajo posible.
Restricciones
Esta es la expresión ∑qic i ≥ a. Son las condiciones que debe cumplir cualquier solución. En este caso, establece que la cobertura total de las cantidades elegidas cumple o supera el área del proyecto. Podríamos añadir muchas más restricciones, y gran parte del poder de la optimización con restricciones reside en la sabia (o incluso inteligente) aplicación de las mismas. De hecho, el dominio de nuestras variables de decisión puede formularse como restricciones.
La función objetivo
Su función objetivo puede ser bastante compleja, pero a medida que se adentra en funciones objetivo más complejas que implican potencias más altas, debe tener en cuenta algunas cosas:
Necesitará un solucionador que pueda manejar ese tipo de problema. Los solucionadores son los que realmente encuentran nuestras soluciones. Algunos solucionadores están pensados para problemas lineales, otros para problemas no lineales, otros se especializan en números enteros, etcétera.
Es posible que no encuentres una solución óptima. En su lugar, puede obtener soluciones factibles o ninguna solución en absoluto.
Puede llevar más tiempo ejecutar la optimización, especialmente en el caso de problemas no lineales.
Hablemos de cada uno de estos problemas por separado.
El solucionador
Los paquetes que manejan optimización con restricciones estarán configurados para tipos específicos de problemas o esperarán que usted les diga qué tipo de solucionador utilizar. A menudo, los paquetes tendrán diferentes solucionadores para elegir, pero a veces se espera que encuentre e instale su propio solucionador.
Encontrar la solución
Algunos problemas de optimización pueden tardar mucho tiempo en resolverse, tanto que no es posible obtener una solución óptima. Para este tipo de problemas, puede terminar con una solución factible, pero no óptima. Eso no es tan malo como parece, porque como el problema es tan complejo, es poco probable que alguien más obtenga una solución óptima. Por supuesto, puede que no obtengas ninguna solución.
Rendimiento
El tiempo de solución para problemas de optimización con restricciones puede variar desde menos de un segundo hasta... bueno, digamos que lo suficientemente largo como para que nadie vaya a esperarlo 😀. Los paquetes actuales son bastante eficientes y, por supuesto, disponemos de una gran potencia de cálculo, pero todavía hay algunos problemas que ponen a prueba incluso al hardware más potente. Para muchas aplicaciones "sencillas" no necesitamos preocuparnos por esto. Pero tenlo en cuenta cuando decidas abordar un problema de optimización con restricciones.
Conclusión
La combinación de función objetivo y restricciones puede abrir la puerta a una gran variedad de problemas que ahora podemos resolver. Y como se dijo anteriormente, hay paquetes por ahí donde podemos darles el problema a resolver y lo harán por nosotros. Hablaré de ello en el próximo artículo. Por ahora, sólo quiero que tengas una visión general de esta clase de problemas y el lenguaje a su alrededor. Quiero hacer esto por las siguientes razones:
Para prepararte para los próximos artículos, en los que profundizaré en el uso de un paquete para resolver este problema.
Para que conozcas la jerga y puedas buscar términos y un lenguaje para expresar tus problemas.
Para aplicar el pensamiento de optimización restringida a los problemas a los que te enfrentas; muchos problemas son de optimización restringida disfrazados o pueden convertirse en ellos.
Sintonízanos la próxima vez, cuando me meta de lleno en el código.